讲座题目：Pólya-type inequalities on spheres and hemispheres
报告专家：毛井教授（湖北大学）
报告时间：2023年9月22日（周五） 下午（16:00—17: 30）
报告地点：理科楼L1218
专家简介：毛井，2013年博士毕业于葡萄牙里斯本大学（Universidade de Lisboa）,2014年4月-2015年3月受国家科技发展委员会（CNPq-Brazil）资助在国家纯粹数学与应用数学研究（Instituto Nacional de Matemtica e Pura Aplicada）从事博士后研究工作。2018年10月---2019年9月受国家留学基金委（CSC-China）资助在里斯本大学进行学术访问。自2013年以来，先后执教于哈尔滨工业大学、湖北大学，现为湖北大学数学与统计学学院教授。目前的主要研究兴趣集中在流形上的谱分析、曲率流及其应用上，在J. Math. Pures Appl., Calc. Var. PDEs, Revista Matemática Complutense, J. Differ. Equations, J. Geom. Anal., Stoch. Proc. Appl., Proc. Amer. Math. Soc., Ann. Glob. Anal. Geom., Chinese Ann. Math. Ser. B等重要国内、国际学术期刊上发表外文论文40余篇。
报告摘要：Given an eigenvalue
of the Laplace-Beltrami on n-spheres or n-hemispheres, with multiplicity m such that
, we characterize the lowest and highest order in the set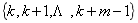
for which Pólya’s conjecture holds and fails. In particular, we show that Pólya’s conjecture holds for hemispheres in the Neumann case, but not in the Dirichlet case when n is greater than two. We further derive Pólya-type inequalities by adding a correction term providing sharp lower and upper bounds for all eigenvalues. This allows us to measure the deviation from the leading term in the Weyl asymptotics for eigenvalues on spheres and hemispheres. As a direct consequence, we obtain similar results for domains which tile hemispheres. We also obtain direct and reversed Li-Yau inequalities for
and 
, respectively. This talk is based on a joint-work with Prof. Pedro Freitas AND Prof. Isabel Salavessa.
English