讲座题目：Multiple solutions for semilinear subelliptic Dirichlet problem

主办单位：三峡数学研究中心/理学院

报告专家：陈化教授（广州大学）

报告时间：2023年5月17日（周三）下午16:00

报告地点：腾讯会议 （ID：477-836-873）

专家简介：陈化，武汉大学数学与统计学院教授，博士生导师，国家杰出青年基金获得者，国务院学科数学评议组第六届和第七届成员，教育部科技委第三届委员会委员。现为武汉大学数学协同创新中心主任，湖北省数学会理事长。陈化的研究方向为偏微分方程的微局部分析理论，退化型偏微分方程，具生物和医学背景的偏微分方程和偏微分方程的谱理论；至今已主持多项国家自然科学基金重点项目，曾为国家重大项目973核心数学项目组成员（2001-2006）并获国家教育部跨世纪优秀人才基金（1998-2000）。陈化至今在国际上专业的SCI数学杂志上发表论文120多篇，曾获国家教育部科技进步二等奖两次，2017年他主持的科研项目获得国家教育部自然科学奖一等奖。

报告摘要：

Let us consider the semilinear subelliptic Dirichlet problem

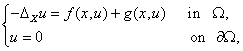
where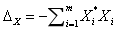is the self-adjoint Hörmander operator associated with vector fields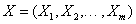satisfying the Hörmander condition, 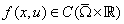, 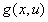is a Carathéodory function on 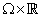, and 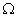is an open bounded domain in 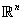with smooth boundary. Combining the perturbation from symmetry method with the approaches involving eigenvalue estimate and Morse index in estimating the min-max values, we obtain two kinds of existence results for multiple weak solutions to the problem above. Furthermore, we discuss the difference between the eigenvalue estimate approach and the Morse index approach in degenerate situations. Compared with the classical elliptic cases, both approaches here have their own strengths in the degenerate cases. This new phenomenon implies the results in general degenerate cases would be quite different from the situations in classical elliptic cases.