讲座题目：Decay estimates for fourth-order Schrodinger operators in dimension two

主办单位：三峡数学研究中心/理学院

报告专家：李平博士（长江大学）

报告时间：2022年3月25日（周五） 上五（09:00—12: 00）

报告地点：腾讯会议（ID： 695586 606）

专家简介：李平博士目前的研究方向是调和分析领域中的高阶Schrodinger算子的散射估计与非交换调和分析；在J. Evol. Equ.; Communications on Pure and Applied Analysis； J.Math.Anal.Appl等国际期刊上发表多篇论文。

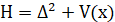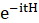报告摘要：In this talk, we study the decay estimates of the fourth-order Schroginger operator                                               on with a bounded decaying potential V(x). We first deduce the asymptotic expansions of resolvent of H near the zero threshold in the presence of resonances or eigenvalue, and then use them to establish the decay estimates of generated by fourth-order Schrodinger operator H. Finally, we classify these zero resonance functions as the distributional solutions of in suitable weighted spaces. Our methods depend on Littlewood-Paley decomposition and oscillatory integral theory. Moreover, due to the degeneracy of 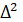at zero threshold and the lower even dimension (i.e.n=2), we remark that the asymptotic expansions of resolvent and the classifications of resonances are more involved than Schrodinger operator 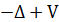in dimension two.