讲座题目:Inverse mean curvature flow for spacelike graphic hypersurfaces with boundary in Lorentz-Minkowski space 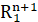 .
.
主办单位:三峡数学研究中心/理学院
报告专家:毛井博士(湖北大学)
报告时间:2021年10月8日(周五)上午(10:00—12: 00)
报告地点:腾讯会议(ID: 504 913 756)
专家简介:毛井,2013年博士毕业于葡萄牙里斯本大学(Universidade de Lisboa),2014年4月-2015年3月受国家科技发展委员会(CNPq-Brazil)资助在国家纯粹数学与应用数学研究(Instituto Nacional de Matemtica e Pura Aplicada)从事博士后研究工作。2018年10月---2019年9月受国家留学基金委(CSC-China)资助在里斯本大学进行学术访问。自2013年以来,先后执教于哈尔滨工业大学、湖北大学,现为湖北大学数学与统计学学院教授。目前的主要研究兴趣集中在流形上的谱分析、曲率流及其应用上,在J. Math. Pures Appl., Calc. Var. PDEs, Revista Matemática Complutense, J. Differ. Equations, J. Geom. Anal., Stoch. Proc. Appl., Proc. Amer. Math. Soc., Ann. Glob. Anal. Geom., Chinese Ann. Math. Ser. B等重要国内、国际学术期刊上发表外文论文40余篇。
报告摘要:In this talk, we introduce the evolution of spacelike graphic hypersurfaces defined over a convex piece of hyperbolic plane 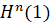 ,
,
of center at origin and radius 1, in the (n+1)-dimensional Lorentz -Minkowski space 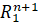 along the inverse mean curvature flow with the vanishing Neumann boundary condition, and show that this flow exists for all the time. Moreover, we can also show that, after suitable rescaling, the evolving spacelike graphic hypersurfaces converge smoothly to a piece of hyperbolic plane of center at origin and prescribed radius, which actually corresponds to a constant func-
along the inverse mean curvature flow with the vanishing Neumann boundary condition, and show that this flow exists for all the time. Moreover, we can also show that, after suitable rescaling, the evolving spacelike graphic hypersurfaces converge smoothly to a piece of hyperbolic plane of center at origin and prescribed radius, which actually corresponds to a constant func-
tion defined over the piece of 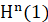 , as time tends to infinity. This talk is based on a joint-work with Dr. Ya Gao.
, as time tends to infinity. This talk is based on a joint-work with Dr. Ya Gao.
